Fine Particles Filtration Equipment
一、工作原理:
含湿气体以较高的流速进入设备水腔中,其液滴被瞬时去除的过程:
1.对于废气中的液滴,可以直接通过溶入水中而被去除。
2.对于废气中的含有液滴的气泡,由于其在水中的快速运动所造成的阻力大于气泡的表面张力,导致气泡破裂。随即气泡中的液滴溶入水中而被去除。另外,由于离心力的作用,气泡中的液滴会不断的撞击到气泡壁上。
当气流速度在30m/s的情况下,可以使直径小于2μm的气泡破裂,从而使直径小于2μm的液滴溶入水中而被去除。另外,在这个速度下,对于直径小于2μm的气泡,液滴运动到气泡壁的时间在10-5s量级,而气泡停留在水中的时间在1s量级。这两种作用共同导致直径小于2μm的液滴溶入水中。
(分析计算见附录一)
二、水腔中的水流翻滚下落溅射出的液滴去除阐述:
1.对于直径大于或等于20μm的液滴,在经过第一道填料处理后,就会去除。
2. 水流翻滚下落溅射出的液滴的尺寸一般大于2μm。
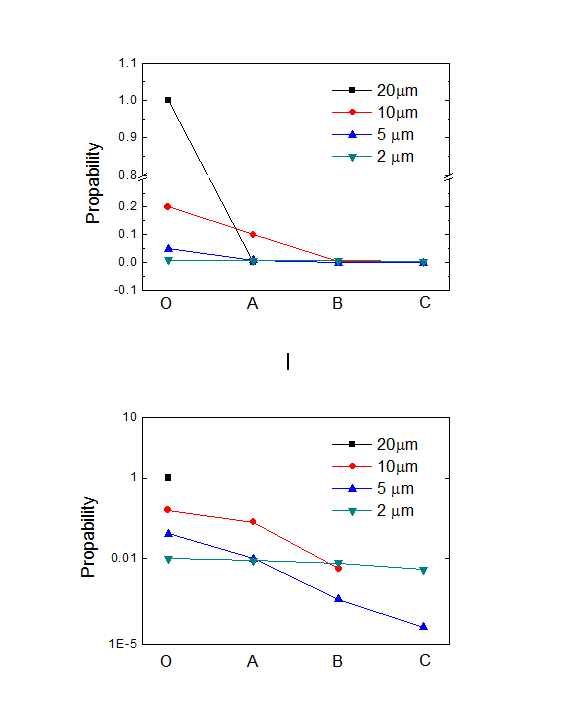
下图为不同尺寸的水滴在不同位置存在的几率(分析计算见附录二):
附录一:
湿气以较高的流速喷入设备中的水腔中,液滴的去除的计算分析
1. 气泡在水中的快速运动造成的阻力大于气泡的表面张力导致气泡破裂的计算分析:
(1)含有液滴的气泡的表面张力:
Pg=2γ/r (1.1)
其中, Pg:气泡表面张力,γ:表面张力系数(0.073N/m), r:气泡半径。
(2)含有液滴的气泡在水中运动受到的阻力(压强):
Po= 1/4 CD ρ v2 (1.2)
其中, Po: 气泡在水中运动受到的阻力(压强),CD:阻力系数, ρ:液体密度, v:气泡相对于水的速度。
(3)阻力系数CD 分别采用Lamb 和Levich的阻力系数值,
当Re≤1 时,CD= 24/Re[( 3μ+2)/ ( 3μ+3)]
当Re>1 时,CD=48/Re (1.3)
其中,Re:雷诺数
(4)雷诺数Re,
Re=ρvd/μ, (1.4)
其中, v:气泡流速,ρ:流体的密度,μ:黏性系数(0.001m Pa),d:特征长度(这里是气泡直径2r)。
根据以上公式推导计算得到:
(1)对于气泡相对于水的流速为30m/s,包裹有微小液滴的半径为1μm的气泡, 其表面张力Pg为 1.4x105 Pa,而其所受的阻力压强为1.8x105 Pa,另外,再加上离心力的影响。因此,导致该气泡破裂,从而使直径小于2μm的液滴溶入水中而被去除。
(2)对于包裹有微小液滴的半径为10μm的气泡,气泡相对于水的流速为10m/s,就足够导致该气泡破裂,从而使液滴溶入水中而被去除。
2. 离心力导致气泡中的液滴碰撞到气泡壁的计算分析:
(1)气泡中的液滴收到的离心力:
F=m.v2/R=m.a (2.1)
其中, F:离心力,m:液滴质量,v:液滴运动速度,R:液滴运动的半径 (0.5m), a:液滴的加速度;
(2)液滴运动到气泡壁的时间:
T=√2S/a=√2S.R/v2 (2.2)
其中, T: 液滴运动到气泡壁的时间,S:液滴到气泡壁的距离(可以近似为气泡的半径)
这里,把气泡中的气体对液滴的阻力忽略了。
根据以上公式推导计算得到,以气泡相对于水的流速为30m/s为例,对于不同直径的气泡,液滴碰撞到气泡壁的时间如下:
气泡直径(μm) | 液滴到气泡壁的时间(s) |
2 | 3.3×10-5 |
1 | 2.3×10-5 |
0.5 | 1.7×10-5 |
0.2 | 1.0×10-5 |
气泡停留在水中的时间在1s量级。因此,直径小于2μm的气泡中的液滴也会因为碰到气泡壁而消失。
附录二:
水腔中的水流翻滚下落溅射出的液滴去除的计算分析
1.液滴在容器气流中的运动速度:
假定:(1)液滴尺寸不变;(2)液滴为球形单一颗粒
液滴稳定后的速度:
Vl=Va-[8r(ρl- ρa)g/3ρaC]1/2 (1)
其中,Va: 气流速度 4m/s,r: 液滴半径;ρl:液滴密度 1000 Kg/m3
ρa:气体密度 1.29 Kg/m³; g:重力加速度 9.81 m/s2;C:阻力系数 0.5
不同液滴尺寸的速度:
Vl=4-201.26 r1/2 (2)
液滴直径(μm) | 液滴半径(μm) | 液滴速度(m/s) |
200 | 100 | 2 |
100 | 50 | 2.58 |
50 | 25 | 3 |
20 | 10 | 3.36 |
10 | 5 | 3.55 |
5 | 2.5 | 3.68 |
2 | 1 | 3.8 |
2.液滴在容器不同区域内的存在的几率 P:
首先,不同直径液滴的分布按照正态分布,
其次,对于直径大于或等于20μm的液滴,在经过第一道填料处理后,就会去除。
A区域: PA=[1-1×(D/20)×(3.36/ Vl)] PO
B区域: PB=[1-1×(D/10)×(3.36/ Vl)] PA
C区域: PC=[1-1×(D/5) ×(3.36/ Vl)] PB
液滴直径(μm) | 在O区存在的几率 PO | 在A区存在的几率 PA | 在B区存在的几率 PB | 在C区存在的几率 PC | 备注 |
20 | 1 | 0 | 0 | 0 | 填料去除 |
10 | 20% | 10% | 0.5% | 0 | 填料去除 |
5 | 5% | 1% | 0.05% | 0.005% | 填料去除 |
2 | 1% | 0.91% | 0.75% | 0.48% | 填料去除 |
≤2 | 0.001% | 0.001% | 0.001% | 0.001% | 撞击水去除 |


